1. Задание № 120 

Сложность: V
Классификатор алгебры: 3\.9\. Рациональные уравнения
Методы алгебры: Использование свойств функций
Рациональные уравнения
i
Решите уравнение
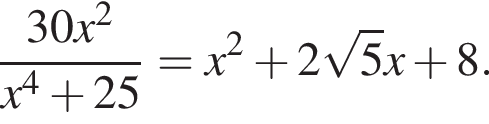
В ответ запишите значение выражения ![]() где x — корень уравнения.
где x — корень уравнения.
Решение. Разделим уравнение на две части — левую и правую: 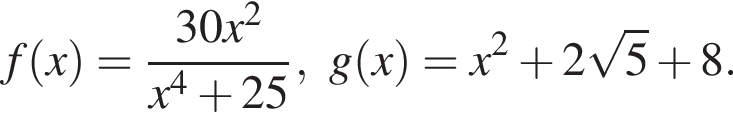
Заметим, что 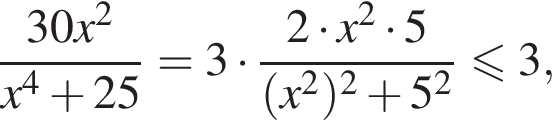 равенство достигается при
равенство достигается при 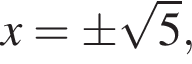 тогда
тогда 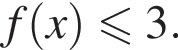
Рассмотрим  равенство достигается при
равенство достигается при 
Тогда левая и правая части равны лишь при  Следовательно,
Следовательно, 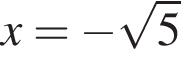 — единственный корень уравнения, тогда:
— единственный корень уравнения, тогда: 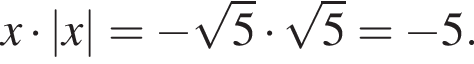
Ответ: −5.
Ответ: -5
120
-5
Сложность: V
Классификатор алгебры: 3\.9\. Рациональные уравнения
Методы алгебры: Использование свойств функций
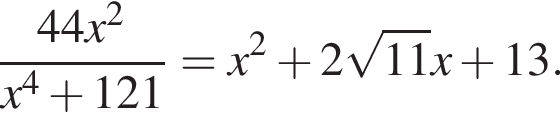
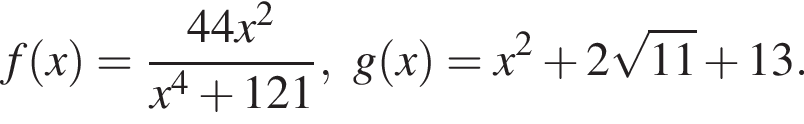
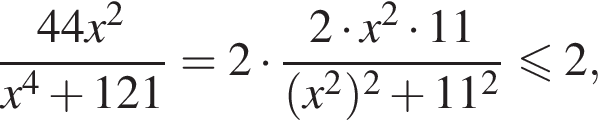 равенство достигается при
равенство достигается при  тогда
тогда 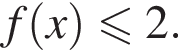
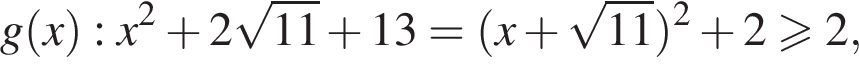
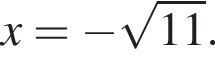
 — единственный корень уравнения, тогда:
— единственный корень уравнения, тогда: 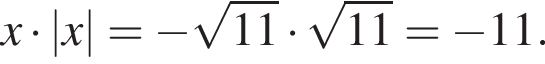
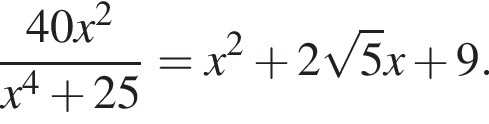
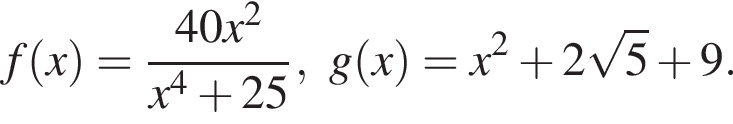
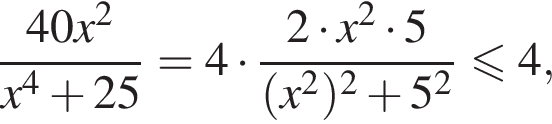 равенство достигается при
равенство достигается при 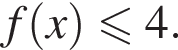
 равенство достигается при
равенство достигается при 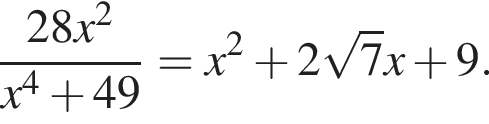
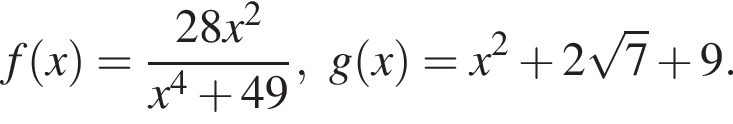
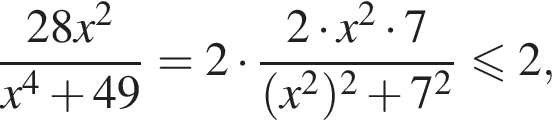 равенство достигается при
равенство достигается при 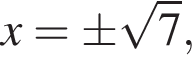 тогда
тогда  равенство достигается при
равенство достигается при 
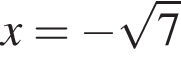 — единственный корень уравнения, тогда:
— единственный корень уравнения, тогда: 
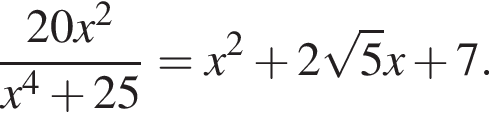
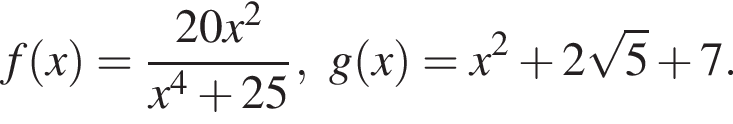
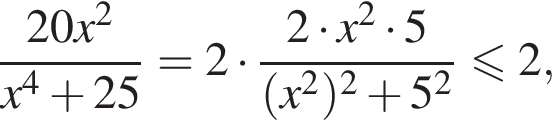 равенство достигается при
равенство достигается при  равенство достигается при
равенство достигается при